Connected Numbers

I was recently shown this puzzle:

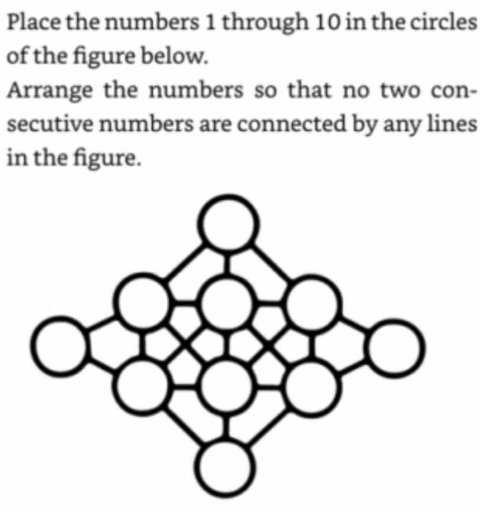
There are some things I found a little unclear about it. For example, should the following two circles count as being connected?

There is a line between them, even if it’s interrupted by a circle.

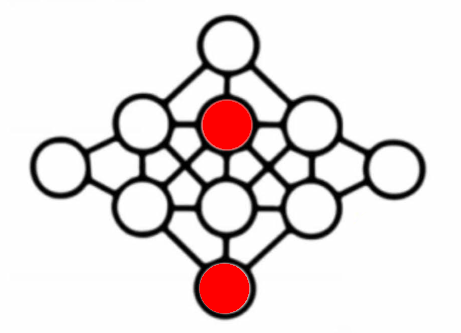
And what about these two circles? Are they connected?

Again, there’s a diagonal line between them. There’s a kink in the line, but is that a quirk of the artwork, or an intentional sign that they should not be consided connected?

The Loosest Restrictions

I started off by looking at the loosest version of the puzzle, where only direct connections between circles are forbidden from having consecutive numbers. That is, the blue circles are not considered connected to each other, and the red circles are not considered connected to each other.

Manually experimenting with pencil and paper, solutions seemed pretty easy to find.

There are some heuristics (guiding principles) that can help you when manually hunting for solutions. Not all the numbers between 1 and 10 are equally tricky to place. The numbers 2 to 9 have consecutive numbers at either side (2 has both 1 and 3 as consecutive numbers). 1 and 10 only have one neighbour each, so you can use that to your advantage by putting them in the more challenging circles. Which circles are the most challenging? Those with the most connections, of course!

Here are some sample solutions:

• A=8 B=5 C=10 D=4 E=3 F=2 G=7 H=1 I=6 J=9
• A=7 B=4 C=10 D=5 E=9 F=3 G=2 H=8 I=1 J=6
• A=8 B=4 C=10 D=3 E=9 F=6 G=2 H=7 I=1 J=5

Note that some solutions are kind of equivalent. If you have a solution, you can flip the board horizontally or vertically (or both!) and it will still work. So the number of possible solutions will always be a multiple of four.

Spoiler alert: I later figured out there are 3968 possible solutions to this version of the puzzle.

This puzzle turned out to be pretty easy, and it seemed more likely that tighter restrictions were meant.

Tighter Restrictions

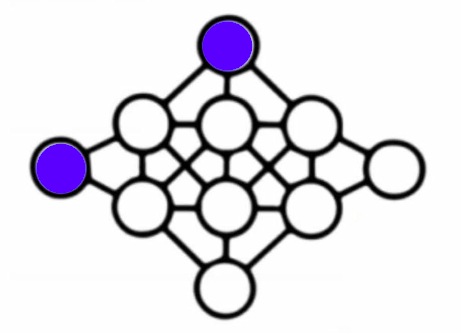
I tightened the restrictions so that circles in the same vertical column or horizontal row were considered connected too. So in the illustrations above, the red circles were connected, but the blue circles connected by a bent diagonal line were not considered connected.

Here things get a lot more tricky and I wasn’t finding any solutions by hand. However, I was convinced that the loosest restrictions were far too easy, so the puzzle maker must have intended for tighter restrictions, so they probably existed. I decided to turn to a programmatic search for solutions.

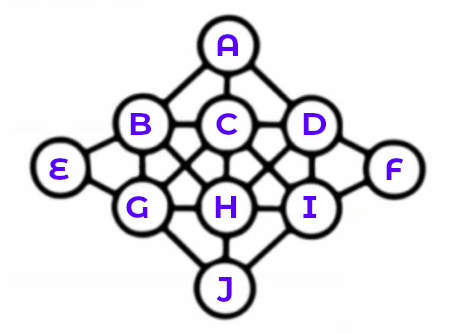
First, I wrote out which circles should be considered connected.

So E, for example, is connected to B and G. There’s some redundancy in this data, because B is connected to E too (the connections are in both directions), but we’re going to take advantage of that later.

Next comes the code.

How it works is that it first compiles a “checker”. The checker is a very simple function which does a bunch of checks like:

return if $E == 1 + $B;   # i.e. return a false value
return if $E == 1 + $G;

And only returns a true value if it hasn’t encountered any conditions where it needs to return false. Note that the checker only needs to check if $E is 1+$B or 1+$G. It doesn’t also need to check if $E is $B-1 and $G-1 because those will be taken care of when $B and $G are checked. That’s where we take advantage of that redundancy!

After that, we use Algorithm::Permute to cycle through every possible arrangement of the numbers 1 to 10, and apply the checker to it, noting which ones pass.

Turns out there are 88 solutions to this version of the puzzle. Again, this is a multiple of four for the same reasons stated earlier. Some sample solutions:

• A=7 B=9 C=1 D=5 E=4 F=2 G=6 H=3 I=8 J=10
• A=9 B=7 C=1 D=5 E=4 F=2 G=10 H=3 I=8 J=6
• A=6 B=8 C=1 D=4 E=2 F=9 G=5 H=10 I=7 J=3

Tightest Restrictions

The tightest restrictions also mean that these circles should be considered connected, even though the line between them is a little bent.

We can use the same code as before to find solutions, just adding the following extra connections:

Even with these restrictions, there are still 40 possible solutions to the puzzle. Some example solutions:

• A=7 B=9 C=1 D=5 E=4 F=2 G=6 H=3 I=8 J=10
• A=9 B=7 C=1 D=5 E=4 F=2 G=10 H=3 I=8 J=6
• A=6 B=10 C=1 D=8 E=4 F=2 G=7 H=3 I=5 J=9

Note that the first two of the above solutions were also listed as solutions to the previous version of the puzzle. That’s because any solutions to the tightest version of the puzzle are also solutions to the earlier versions.

This puzzle was a bit of fun to solve, even if the brute force approach could be regarded as cheating!